Finding the length of the loop in the linked list using C/C++/Python/Java
Finding the length of the loop in a linked list using different programming languages. Different programming languages have only a small difference in syntax. It is a loop, inside which we have nodes.
In C++:
It is the language used to develop games. To calculate the length of loop in linked list:
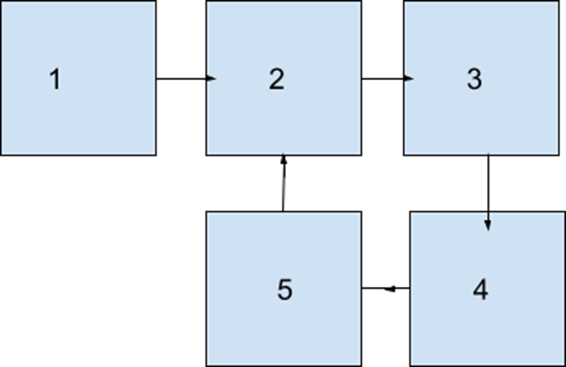
Floyd’s Cycle Finding Algorithm is used where we have to traverse the linked list using two pointers. The slow pointer used will increase by 1 and the fast pointer used will increase by 2, if these numbers meet then it checks whether a loop exists or not.
Now, a loop may also contain some statements or nodes and will return zero if there is no loop.
#include<bits/stdc++.h> using namespace std;
struct loopin {
int data;
struct loopin*next;
};
int countLooppoints(struct loopin *n)
{
int r = 1;
struct loopin *t = n; while (t->next != n) {
r++;
t = t->next;
}
return r;
}
int countLoopLoopin(struct loopin *list)
{
struct loopin *slowPtr = list, *fastPtr = list; while (slowPtr && fastPtr && fastPtr->next) {
slowPtr = slowPtr->next; fastPtr = fastPtr->next->next;
if (slowPtr == fastPtr) //that means a loop exists// return countLooppoints(slowPtr);
}
return 0; //when there is no loop inside it//
}
struct loopin *newloopin(int key)
{
struct loopin *t = (struct loopin*)malloc(sizeof(struct loopin)); t->data = key;
t->next = NULL; return t;
}
int main()
{
struct loopin *head = newloopin(1); head->next = newloopin(2);
head->next->next = newloopin(3);
head->next->next->next = newloopin(4);
head->next->next->next->next = newloopin(5); head->next->next->next->next->next = head->next;
cout<<"The number of loops linked inside the loop are "<<countLoopLoopin(head);
return 0;
}
The output :
The number of loops linked inside the loop are 4
In C :
C uses printf() and scanf() to give output and take input respectively while C++ uses cin() and cout() to take input and output respectively. C does not contain classes and objects while c++ contains classes and objects.
We use Floyd’s Cycle Finding Algorithm, where we have to traverse the linked list using two pointers. The slow pointer=s_p used will increase by 1 and the fast pointer=f_p used will increase by 2, if these numbers meet at some point then a loop exists.
a loop may also contain some statements or any nodes,using this method we can calculate inside the loop. Here, Loopin are the loops inside the loop.
#include<stdio.h> #include<stdlib.h> struct loopin
{
int data;
struct loopin* next;
};
int countloopin(struct loopin *n)
{
int r = 1;
struct loopin *t = n; while (t->next != n)
{
r++;
t = t->next;
}
return r;
}
int countlooploopin(struct loopin *list)
{
struct loopin *s_p = list, *f_p = list; while (s_p && f_p && f_p->next)
{
s_p = s_p->next;
f_p = f_p->next->next;
if (s_p == f_p)
return countloopin(s_p);
}
return 0;
}
struct loopin* newloopin(int x)
{
struct loopin* loopin = malloc(sizeof(struct loopin*)); loopin->data = x;
loopin->next = NULL; return loopin;
}
int main()
{
struct loopin *head = newloopin(1); head->next = newloopin(2);
head->next->next = newloopin(3);
head->next->next->next = newloopin(4);
head->next->next->next->next = newloopin(5); head->next->next->next->next->next = head->next; int ans = countlooploopin(head);
printf(" the number of loops in loop %d \n",ans); return 0;
}
The output:
The number of loops in loop 4
In Python:
it is a friendly language with many libraries and well-defined functions which makes it easy to use. We use Floyd’s Cycle Finding Algorithm, where we have to traverse the linked list using two pointers. The slow pointer=s_p used will increase by 1 and the fast pointer=f_p used will increase by 2,if these numbers meet at some point then there exists a loop.
A loop may also contain some statements or any nodes. Here, Loopin is the loop inside the loop.
class loop:
def init (self, val): self.val = val self.next = None
class Linkedlist:
def init (self):
self.head = None
def Addloop(self, val): if self.head is None:
self.head = loop(val) else:
curr = self.head while(curr.next):
curr = curr.next curr.next = loop(val)
def countloopinloop(self): p = self.head
pos = 0
m = dict() while p:
if p not in m: m[p] = pos pos += 1
else:
return pos - m[p] p = p.next
return 0
myLL = Linkedlist() myLL.Addloop(1) myLL.Addloop(2) myLL.Addloop(3) myLL.Addloop(4) myLL.Addloop(5)
myLL.head.next.next.next.next.next = myLL.head.next loopLength = myLL.countloopinloop()
if myLL.head is None: print("Linked list is empty")
else:
print(str(loopLength))
The output:
4
In Java:
In Java , output is system.out.printIn() which is the same as system.out.print() . The main.java file is created. It is case sensitive
We use Floyd’s Cycle Finding Algorithm, where we have to traverse the linked list using two pointers. The slow pointer= s_p used will increase by 1 and the fast pointer=f_p used will increase by 2. If these numbers meet at some point, then there exists a loop. A loop may contain some statements or nodes and when the pointers meet, it checks inside the loop. It will return 0 when there is no loop inside it.
import java.io.*; class GFG
{
static class loopin
{
int data; loopin next;
loopin (int data)
{
this.data = data; next = null;
}
}
static int countloops (loopin n)
{
int r = 1; loopin t = n;
while (t.next != n)
{
r++;
t = t.next;
}
return r;
}
static int countloopsinloop (loopin list)
{
loopin s_p = list, f_p = list;
while (s_p != null && f_p != null && f_p.next != null)
{
s_p = s_p.next;
f_p = f_p.next.next;
if (s_p == f_p)
return countloops (s_p);
}
/* Return 0 to indicate that there is no loop */ return 0;
}
static loopin newloopin (int key)
{
loopin t = new loopin (key);
return t;
}
public static void main (String[]args)
{
loopin head = newloopin (1); head.next = newloopin (2); head.next.next = newloopin (3); head.next.next.next = newloopin (4);
head.next.next.next.next = newloopin (5);
/* Create a loop for testing */ head.next.next.next.next.next = head.next;
System.out.println (countloopsinloop (head));
}
}
The output:
4
Complexity Analysis:
- Time complexity:O(n).
Only one traversal of the linked list is needed. - Auxiliary Space:O(1).
As no extra space is required.