In Class 12 Boards there will be Case studies and Passage Based Questions will be asked, So practice these types of questions. Study Rate is always there to help you. Free PDF Download of CBSE Class 12 Mathematics Chapter 9 Differential Equations Case Study and Passage Based Questions with Answers were Prepared Based on Latest Exam Pattern. Students can solve NCERT Class 12 Maths Differential Equations to know their preparation level.
Join our Telegram Channel, there you will get various e-books for CBSE 2024 Boards exams for Class 9th, 10th, 11th, and 12th.
In CBSE Class 12 Maths Paper, There will be a few questions based on case studies and passage-based as well. In that, a paragraph will be given, and then the MCQ questions based on it will be asked.
Differential Equations Case Study Questions With answers
Here, we have provided case-based/passage-based questions for Class 12 Mathematics Chapter 9 Differential Equations
Case Study/Passage Based Questions
A thermometer reading 80°F is taken outside. Five minutes later the thermometer reads 60°F. After another 5 minutes the thermometer reads 50°F. At any time t the thermometer reading be T°F and the outside temperature be S °F.
If λ is positive constant of proportionality, then dT/dt is
(a) λ (T – S) (b)λ (T + S)
(c) λTS (d) –λ (T – S)
Answer: (d) –λ (T – S)
The value of T(5) is
(a) 30°F (b) 40°F (c) 50°F (d) 60°F
Answer: (d) 60°F
The value of T(10) is
(a) 50°F (b) 60°F (c) 80°F (d) 90°F
Answer: (a) 50°F
Find the general solution of differential equation formed in given situation.
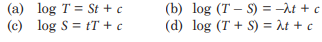
Answer: (b)
Find the value of constant of integration c in the solution of differential equation formed in given situation.
(a) log (60 – S) (b) log (80 + S)
(c) log (80 – S) (d) log (60 + S)
Answer: (c) log (80 – S)
Case Study/Passage Based Questions
It is known that, if the interest is compounded continuously, the principal changes at the rate qual to the product of the rate of bank interest per annum and the principal. Let P denotes the principal at any time t and rate of interest be r % per annum.
Find the value of dP/dt .
(a) Pr/1000 (b) Pr/100 (c) Pr/10 (d) Pr
Answer: (b) Pr/100
If P0 be the initial principal, then find the solution of the differential equation formed in a given situation.
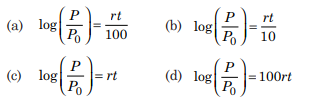
Answer: (a)
If the interest is compounded continuously at 5% per annum, then in how many years will ₹100 double itself ? (loge 2 = 0.6931)
(a) 12.728 years (b) 14.789 years
(c) 13.862 years (d) 15.872 years
Answer: (c) 13.862 years
At what interest rate will ₹ 100 double itself in 10 years? (loge2 = 0.6931).
(a) 9.66% (b) 8.239% (c) 7.341% (d) 6.931%
Answer: (d) 6.931%
How much will ₹ 1000 be worth at 5% interest after 10 years? (e0.5 = 1.648).
(a) ₹ 1648 (b)₹ 1500 (c)₹ 1664 (d) ₹1572
Answer: (a) ₹ 1648
Hope the information shed above regarding Case Study and Passage Based Questions for Class 12 Maths Chapter 9 Differential Equations with Answers Pdf free download has been useful to an extent. If you have any other queries of CBSE Class 12 Mathematics Differential Equations Case Study and Passage Based Questions with Answers, feel free to comment below so that we can revert back to us at the earliest possible.
By Team Study Rate
